为什么要使用概率
在医生诊断病人的例子中,我们用概率来表示一种信任度( degree of belief),其中1表示非常肯定病人患有流感,而0表示非常肯定病人没有流感。前面那种概率,直接与事件发生的频率相联系,被称为频率派概率( frequentist probability);而后者,涉及到确定性水平,被称为贝叶斯概率( Bayesian probability)。
随机变量
随机变量( random variable)是可以随机地取不同值的变量。
随机变量可以是离散的或者连续的。离散随机变量拥有有限或者可数无限多的状态。注意这些状态不一定非要是整数;它们也可能只是一些被命名的状态而没有数值。连续随机变量伴随着实数值。
概率分布
离散型变量和概率质量函数

1 | 也有翻译成概率分布律的 |


连续型变量和概率密度函数


边缘概率

条件概率


条件概率的链式法则

独立性和条件独立性

如果关于x和y的条件概率分布对于z的每一个值都可以写成乘积的形式那么这两个随机变量x和y在给定随机变量z时是条件独立的。
期望、方差和协方差



协方差的绝对值如果很大则意味着变量值变化很大并且它们同时距离各自的均值很远。如果协方差是正的,那么两个变量都倾向于同时取得相对较大的值。如果协方差是负的,那么其中一个变量倾向于取得相对较大的值的同时,另一个变量倾向于取得相对较小的值,反之亦然。其他的衡量指标如相关系数( correlation)将每个变量的贡献归一化,为了只衡量变量的相关性而不受各个变量尺度大小的影响。
协方差和相关性是有联系的,但实际上是不同的概念。它们是有联系的,因为两个变量如果相互独立那么它们的协方差为零,如果两个变量的协方差不为零那么它们一定是相关的。然而,独立性又是和协方差完全不同的性质。两个变量如果协方差为零,它们之间一定没有线性关系。独立性比零协方差的要求更强,因为独立性还排除了非线性的关系。两个变量相互依赖但具有零协方差是可能的。
常用概率分布
Bernoulli分布(01分布)

Multinoulli分布
就是多项分布。
高斯分布
即为正态分布。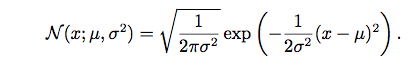
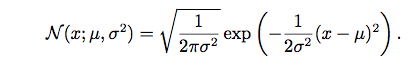
指数分布和 Laplace分布
指数分布
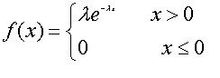
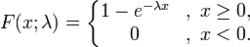
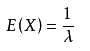
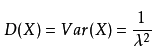
拉普拉斯分布
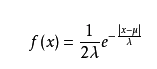
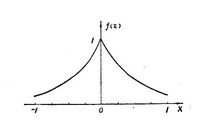
Dirac分布和经验分布
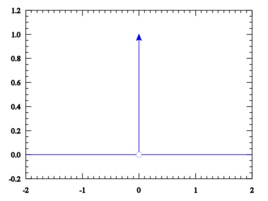
Dirac分布
狄拉克δ函数是一个广义函数,在物理学中常用其表示质点、点电荷等理想模型的密度分布,该函数在除了零以外的点取值都等于零,而其在整个定义域上的积分等于1。
狄拉克δ函数在概念上,它是这么一个“函数”:在除了零以外的点函数值都等于零,而其在整个定义域上的积分等于1。
经验分布

分布的混合
通过组合一些简单的概率分布来定义新的概率分布也是很常见的。一种通用的组合方法是构造混合分布( mixture distribution)。混合分布由一些组件( component)
分布构成。
混合模型是组合简单概率分布来生成更丰富的分布的一种简单策略。
混合模型使我们能够一瞥以后会用到的一个非常重要的概念—潜变量。

常用函数的有用性质
logistic sigmoid函数

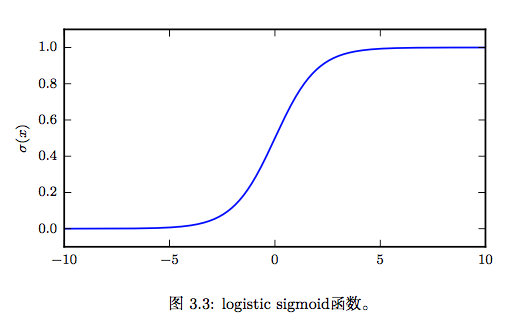
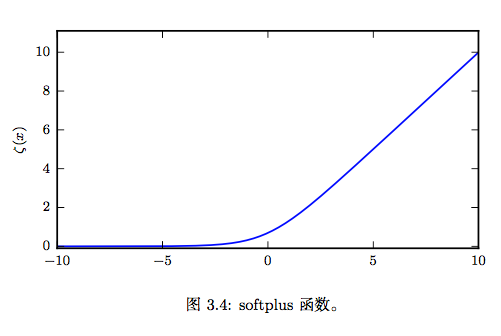
softplus函数
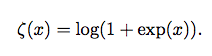
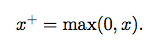


贝叶斯规则

连续型变量的技术细节
连续型随机变量和概率密度函数的深入理解需要用到数学分支测度论(Ineasure heory)的相关内容来扩展概率论。




信息论
信息论是应用数学的一个分支,主要研究的是对一个信号包含信息的多少进行量化。在机器学习中,我们也可以把信息论应用于连续型变量。
信息论的基本想法是一个不太可能的事件居然发生了,要比一个非常可能的事件发生,能提供更多的信息。



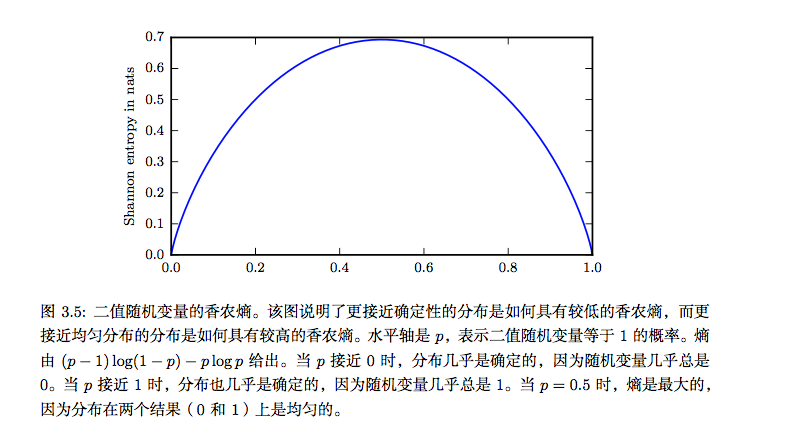
也记作H(P)。换言之,一个分布的香农熵是指遵循这个分布的事件所产生的期望信息总量。当x是连续的,香农熵被称为微分熵( differential entropy)。
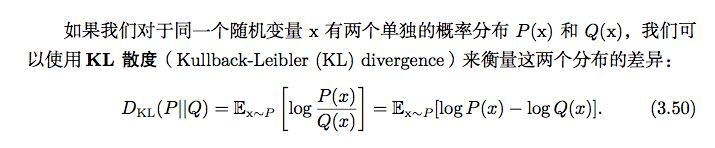
又称为相对熵,是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的比特个数。典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。
是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着D(P||Q) ≠ D(Q||P)。特别的,在信息论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,产生的信息损耗,其中P表示真实分布,Q表示P的拟合分布。
有人将KL散度称为KL距离,但事实上,KL散度并不满足距离的概念,因为:(1)KL散度不是对称的;(2)KL散度不满足三角不等式。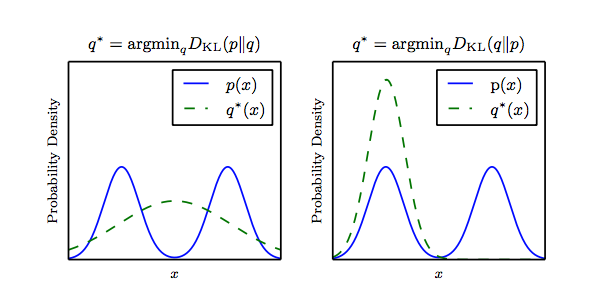

结构化概率模型
机器学习的算法经常会涉及到在非常多的随机变量上的概率分布。通常,这些概率分布涉及到的直接相互作用都是介于非常少的变量之间的。使用单个函数来描述整个联合概率分布是非常低效的 (无论是计算上还是统计上)。
我们可以把概率分布分解成许多因子的乘积形式,而不是使用单一的函数来表 示概率分布。例如,假设我们有三个随机变量 a, b 和 c,并且a影响b的取值,b影响c的取值,但是 a 和 c 在给定 b 时是条件独立的。我们可以把全部三个变量的概 率分布重新表示为两个变量的概率分布的连乘形式: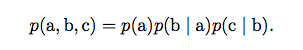
这种分解可以极大地减少用来描述一个分布的参数数量。每个因子使用的参数 数目是它的变量数目的指数倍。
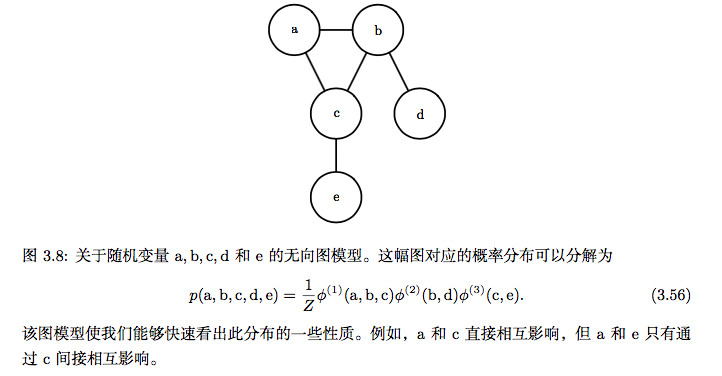
我们可以用图来描述这种分解。把它称为结构化概率模型(structured probabilistic model)或者图模型(graphical model)。
有两种主要的结构化概率模型:有向的和无向的。两种图模型都使用图 G,其中 图的每个节点对应着一个随机变量,连接两个随机变量的边意味着概率分布可以表 示成这两个随机变量之间的直接作用。